Abstract
This project delves into the realm of Structure from Motion (SfM), focusing on 3D scene reconstruction and simultaneous camera pose estimation using monocular camera images. The study explores feature extraction, matching, and epipolar geometry principles to derive the Fundamental matrix and Essential matrix, which play vital roles in establishing point correspondences and camera poses. The project also incorporates Linear and Non-Linear Triangulation techniques to minimize algebraic and geometric errors in 3D point estimation. Finally, Bundle Adjustment is performed to refine camera poses and 3D points, achieving precise localization and mapping results. The combination of these methods leads to a robust and accurate SfM framework, essential for various applications in robotics, computer vision, and 3D modeling.

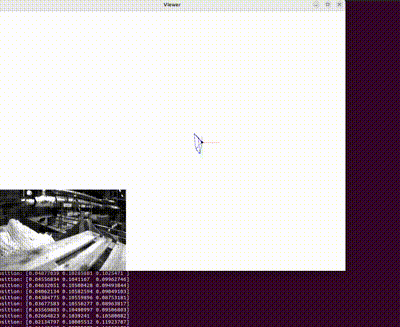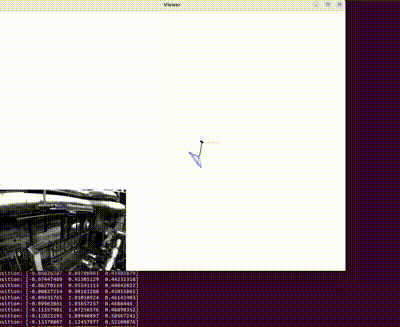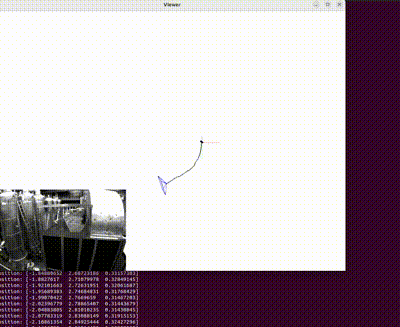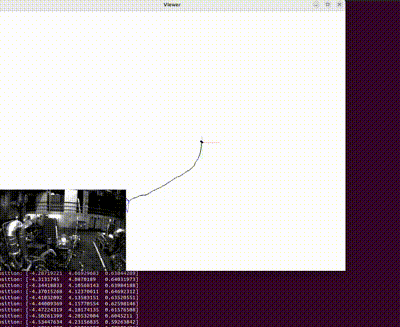
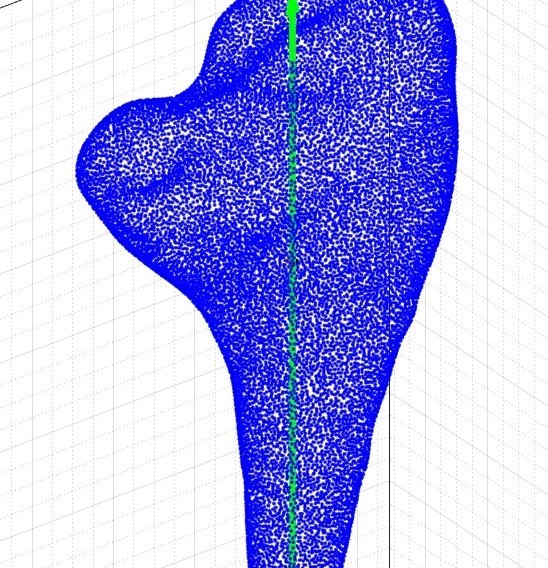
3D Reconstructed Unity Hall, WPI

Feature matching using SIFT
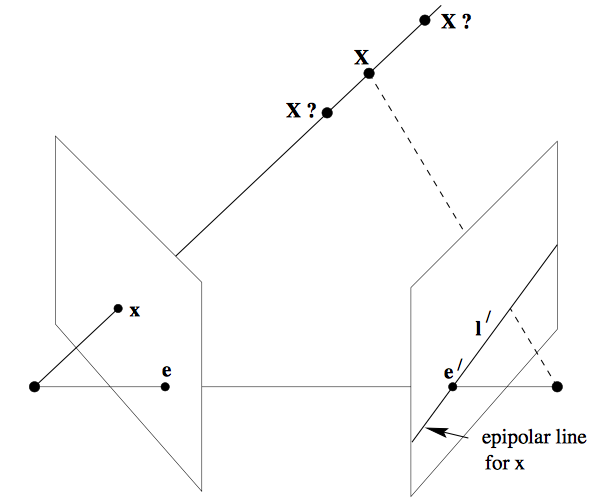
Epipolar Constraint Formulation
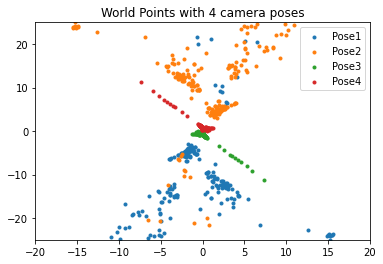
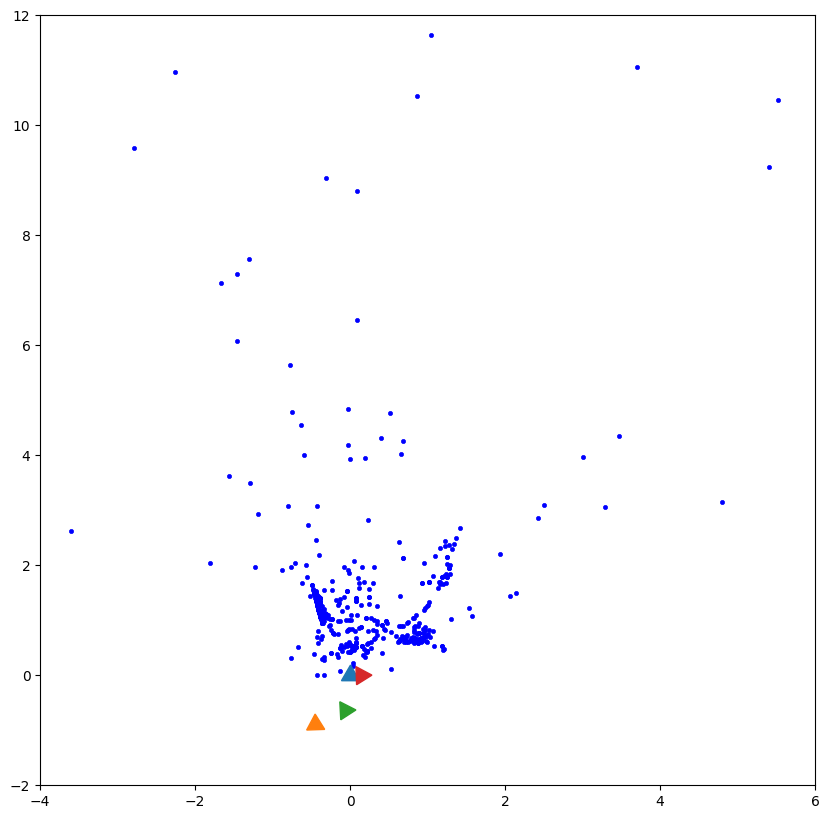
Camera Poses: Triangulation
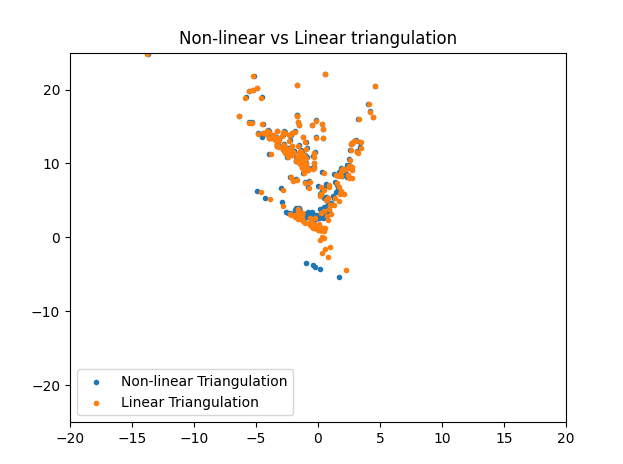
Optimization: Linear vs Non-Linear Triangulation
Bundle Adjustment
Introduction
With a foundation rooted in exploring 2D imagery, this project has led me to an exciting new realm of discovery - Structure from Motion (SfM). Within this domain, my focus has shifted towards the reconstruction of 3D scenes and the simultaneous acquisition of camera poses of monocular camera w.r.t a given scene. The image showcased on the left stands as a testament to the fruits of my hardwork; it exhibits the impeccably reconstructed Unity Hall at WPI, along with the intricate camera poses.
The primary objective of this project revolves around the creation of a complete and coherent rigid structure, leveraging a diverse range of images captured from various viewpoints or, equivalently, through a camera in motion. In undertaking this endeavor, inspiration has been drawn from the groundbreaking work by Agarwal et al., as documented in their publication titled "Building Rome in a Day." In this remarkable study, the authors successfully reconstructed an entire city by harnessing the power of a vast collection of internet-sourced photographs.
Approach to the SfM problem
The dataset utilized for this project encompassed a collection of monocular images captured while in motion. These images were obtained using the primary camera of a Samsung S22 Ultra smartphone, with a fixed focus setting. The camera settings were optimized to achieve optimal image quality, employing an aperture of f/1.8, ISO 50, and a shutter speed of 1/500 seconds. Notably, the provided images have already undergone distortion correction and have been resized to dimensions of 800x600 pixels.
Given the vital role that feature extraction and matching play in the Structure from Motion process, a robust approach was adopted in this project. Specifically, keypoint matching was implemented using SIFT (Scale-Invariant Feature Transform) keypoints and descriptors. The utilization of these techniques enhances the reliability and accuracy of the feature matching process, thereby contributing to the overall success and effectiveness of the project.
Epipolar Geometry
Once keypoint matching has been established using SIFT and the matches further refined through the application of the Random Sample Consensus (RANSAC) algorithm to eliminate outliers, the primary objective shifts towards determining correspondences between points in the form of the Fundamental matrix.
The Fundamental matrix, a rank 2, 3x3 matrix with seven degrees of freedom, plays a crucial role in expressing the relationship between corresponding image points, leveraging the principles of epipolar geometry. By utilizing the concept of the epipolar constraint, or Longuet-Higgins equation (x'ᵀFₓ = 0), a homogeneous linear system with nine unknowns - the elements of the Fundamental matrix - can be constructed. Through the pursuit of this homogeneous linear system, the goal of deriving the precise fundamental matrix is accomplished, which plays a vital role in the accurate determination of correspondences between image points.
Entering the 3rd Dimension
Once the fundamental matrix has been derived using the eight-point algorithm and Longuet-Higgins equation, it is necessary to perform Fundamental matrix decomposition via Singular Value Decomposition (SVD). With this task accomplished, the focus shifts from point correspondences between images to establishing a connection between the images and the 3D world. To achieve this, a fundamental matrix that relates the corresponding points, assuming adherence to the pinhole camera model, is required.
Herein lies the utility of the Essential Matrix, which is expressed mathematically as E = KᵀFK, where K is the camera calibration or intrinsic matrix. It is essential to note that while F is defined in original image space (i.e., pixel coordinates), E is expressed in normalized image coordinates. Therefore, a correction must be performed while executing the SVD.
Locating Camera Poses and Triangulations
To sum up so far, the use of the Fundamental Matrix is predominant in uncalibrated methods, whereas the Essential Matrix is favored in calibrated methods. From the corresponding 3D points, the crucial step is to perform triangulation. By taking into account corresponding image points, x1 and x2, from two different viewpoints, and their respective camera projection matrices, P1 and P2, the computation of the 3D point X is achieved through solving a linear system. The Linear Triangulation method, which utilizes algorithms like the Direct Linear Transform (DLT), is commonly employed for this purpose, where a system of equations is established, and X is estimated through homogeneous coordinates.
Once the E matrix is identified, it becomes possible to compute four potential camera pose configurations: (C1,R1), (C2,R2), (C3,R3), and (C4,R4), where C∈R3 represents the camera center and R∈SO(3) denotes the rotation matrix. However, it is essential to validate the accuracy of the camera poses by satisfying the "chierality constraint" or the "depth positivity constraint." These constraints ensure that the camera poses align with the correct spatial arrangement and maintain a positive depth relationship with the scene being captured.
Optimization
Triangulation in Structure from Motion (SfM) involves two key steps: Linear Triangulation and Non-Linear Triangulation. Linear Triangulation aims to minimize the algebraic error by estimating the 3D positions of points based on their 2D projections and the known camera parameters. However, this method may still result in geometric errors due to noise in the feature matching process. To address this, Non-Linear Triangulation is performed, which further minimizes the geometric error or the reprojection error.
In scenarios where multiple images are available, Perspective-n-Point (PnP) algorithms are employed. These algorithms optimize both linear and non-linear re-projection errors to accurately estimate camera poses and 3D points. By considering the 2D-3D correspondences and intrinsic camera parameters, PnP enables the determination of camera poses and scene geometry.
To obtain the final refined output, Bundle Adjustment is conducted, leveraging the visibility matrix. Bundle Adjustment optimizes camera poses and 3D points by simultaneously minimizing the re-projection error across all parameters. This comprehensive optimization process ensures the best possible results by iteratively refining the camera poses and 3D point positions to achieve optimal alignment between the observed 2D projections and the reconstructed 3D points.